Jak obliczyć metry sześcienne? Wzór i kalkulator online

Jeśli zastanawiasz się, jak obliczyć metry sześcienne, jesteś w dobrym miejscu. Ta umiejętność przydaje się częściej, niż myślisz – od planowania przeprowadzki, przez zakup drewna opałowego, aż po obliczenie kubatury pokoju przed montażem klimatyzacji. W tym poradniku pokażę Ci, jak szybko policzyć objętość różnych kształtów, jakich wzorów używać i na co szczególnie uważać, aby nie przepłacić ani nie popełnić prostych błędów. Dzięki prostym zasadom i jasnym wskazówkom zaczniesz sprawnie przeliczać m³ w każdej sytuacji i podejmować lepsze, bardziej świadome decyzje. Zobacz!

Czym są metry sześcienne (m³)? 

Metry sześcienne pozwalają określić realną ilość przestrzeni, jaką coś zajmuje lub może pomieścić. To jedna z najbardziej praktycznych jednostek w codziennych obliczeniach – pomaga Ci przewidzieć, czy coś się zmieści, ile materiału potrzebujesz albo czy transport będzie opłacalny.

Definicja objętości

Objętość to miara przestrzeni trójwymiarowej, którą zajmuje dany obiekt. Mówimy tu o połączeniu trzech wymiarów: długości, szerokości i wysokości. Jeden metr sześcienny to sześcian o bokach długości jednego metra, a więc 1 m × 1 m × 1 m. W praktyce oznacza to możliwość dokładnego opisania, ile fizycznej przestrzeni zajmuje lub pomieści dany przedmiot, niezależnie od jego kształtu.

Kiedy stosujemy jednostkę m³?

Jednostka m³ jest stosowana wszędzie tam, gdzie liczy się przestrzeń, pojemność lub masa materiału powiązana z jego objętością. Wykorzystujesz ją przy obliczaniu kubatury pomieszczeń, planowaniu transportu, wycenie drewna opałowego, a także przy zakupie materiałów, takich jak żwir, piasek, woda czy beton. Dzięki przeliczaniu na metry sześcienne możesz szybko ocenić, czy dany towar spełni Twoje potrzeby i czy jego ilość jest odpowiednio dobrana.

Jak obliczyć metry sześcienne? Podstawowe wzory

Aby sprawnie ustalić, jak obliczyć metry sześcienne, potrzebujesz tylko kilku prostych wzorów dopasowanych do kształtu obiektu. Dzięki nim szybko przeliczysz objętość niezależnie od tego, czy mierzysz pokój, rurę, beczkę czy materiały sypkie.

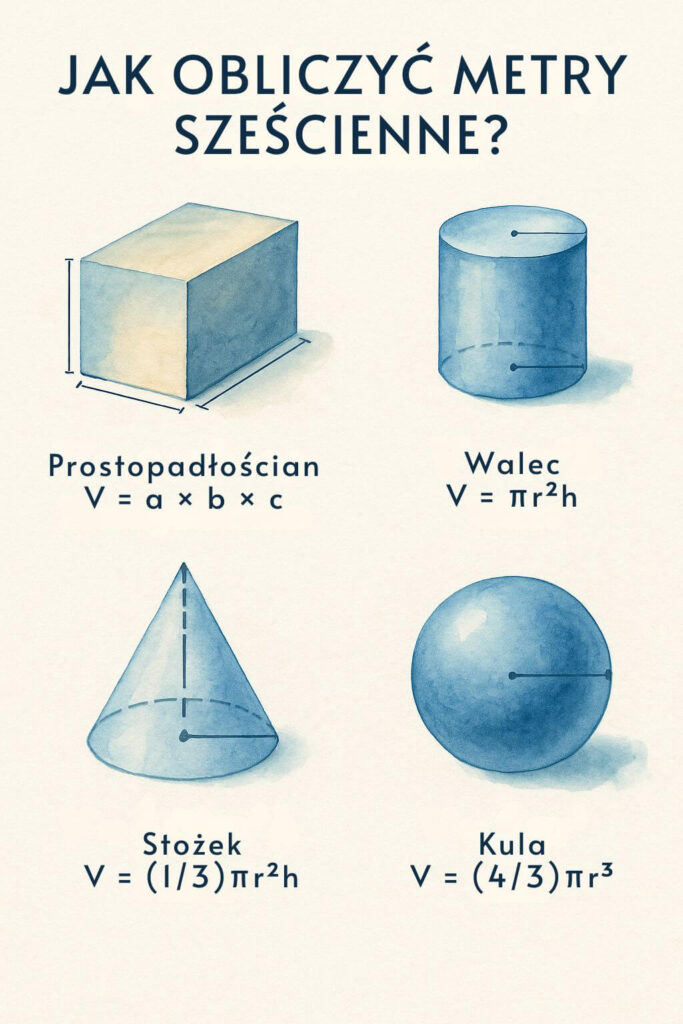
Prostopadłościan (kostka, pudełko, pokój)

To jeden z najłatwiejszych kształtów do obliczenia objętości, ponieważ opiera się wyłącznie na trzech prostych wymiarach, które możesz zmierzyć nawet zwykłą miarką.

Wzór: V = a × b × c

Objętość wyznaczasz, mnożąc długość, szerokość i wysokość. Ten wzór sprawdzi się idealnie wszędzie tam, gdzie masz do czynienia z prostymi płaskimi ścianami i krawędziami. Jeśli któryś z wymiarów podajesz w centymetrach, pamiętaj o przeliczeniu na metry, aby uniknąć błędnych wyników.

Znaczenie parametrów: długość, szerokość, wysokość

Każdy z wymiarów określa jedną z trzech osi przestrzeni – a ich iloczyn daje finalną objętość. Dokładny pomiar to klucz, zwłaszcza w pomieszczeniach, gdzie często wysokość bywa różna na różnych ścianach. Jeśli obiekt ma nieregularny kształt, możesz podzielić go na mniejsze prostopadłościany i policzyć każdy osobno.

Sytuacje praktyczne zastosowania

Wzór ten wykorzystasz przy obliczaniu kubatury pokoju, szopy, garażu, skrzyń transportowych, kartonów czy mebli. Jest też podstawą w logistyce – pozwala ocenić, ile ładunku zmieści się w busie, kontenerze czy magazynie.

Walec (np. beczka, rura)

Walec występuje w wielu sytuacjach: od pojemników na wodę po rury wentylacyjne i zbiorniki techniczne.

Wzór: V = πr²h

Objętość otrzymujesz, mnożąc pole koła będącego podstawą walca przez jego wysokość. Warto pamiętać, że mały błąd w promieniu daje duży błąd w końcowym wyniku, bo promień jest podnoszony do potęgi drugiej.

Podstawa: koło i promień

Pole podstawy wynika z promienia – połowy średnicy. Jeśli mierzysz średnicę, podziel ją na dwa, zanim wstawisz r do wzoru. Gdy podstawa nie jest idealnie okrągła (np. lekko zdeformowana beczka), najlepiej zmierzyć średnicę w kilku miejscach i uśrednić wynik.

Wysokość walca

To odległość między górną a dolną podstawą, mierzona pionowo. W przypadku rur montowanych w terenie warto sprawdzić wysokość w dwóch-trzech punktach, bo podłoże może być nierówne. Dokładny pomiar daje pewność, że objętość będzie policzona poprawnie.

Stożek

Stożki kojarzą się głównie z lejkami, ale występują też w silosach, lejach transportowych i naturalnych hałdach materiałów.

Wzór: V = (1/3)πr²h

Objętość stożka to jedna trzecia objętości walca o tych samych parametrach. Dzięki temu możesz łatwo porównać oba kształty i ocenić, ile materiału mieści się w stożkowym zbiorniku.

Podstawa i wysokość

Podstawa jest kołem, więc kluczowy jest dokładny pomiar promienia. Wysokość musi być mierzona pionowo od wierzchołka do środka podstawy – nie po skosie ścianki. Ten błąd pomiarowy zdarza się często i potrafi całkowicie zniekształcić wynik.

Typowe zastosowania (np. lejki, hałdy)

Wzór wykorzystasz przy wyliczaniu objętości lejków zsypowych, lejów przemysłowych, stożkowych silosów czy hałd piasku, żwiru i węgla. To również przydatne przy analizie stosów materiałów sypkich na budowie lub w ogrodzie.

Kula

Kształt kuli spotkasz w zbiornikach ciśnieniowych, balonach technicznych czy dekoracjach, a obliczanie jej objętości jest prostsze, niż wygląda.

Wzór: V = (4/3)πr³

Objętość kuli zależy wyłącznie od promienia podniesionego do trzeciej potęgi, dlatego nawet niewielkie różnice w pomiarze mają duże przełożenie na wynik. To szczególnie ważne przy zbiornikach, gdzie pojemność musi być precyzyjna.

Promień kuli

Promień to połowa średnicy mierzona przez środek kuli. Jeśli mierzysz obiekt elastyczny, jak balon czy piłka, warto wykonać kilka pomiarów w różnych kierunkach i obliczyć średnią – zapewni to dokładniejszy wynik.

Przykłady zastosowania

Formuły tej użyjesz przy obliczaniu pojemności balonów płynowych, zbiorników kulistych, elementów dekoracyjnych czy kul stosowanych w technice i przemyśle. Pozwala to przewidzieć pojemność i dopasować ją do realnych potrzeb.

Jednostki objętości i przeliczanie na metry sześcienne

Aby wiedzieć dokładnie, jak obliczyć metry sześcienne, warto najpierw zrozumieć, jak działają najpopularniejsze jednostki objętości i w jaki sposób można je szybko przeliczać. Dzięki temu unikniesz błędów i łatwo porównasz różne wartości.

Podstawowe jednostki objętości

Objętość można wyrażać w kilku jednostkach, a każda z nich sprawdza się w innych zastosowaniach. Znajomość ich skali pozwala lepiej interpretować wyniki pomiarów.

Litr

Litr to jednostka, którą spotykasz na co dzień – w kuchni, garażu czy sklepie. Odpowiada objętości sześcianu o boku 10 cm, czyli 1000 centymetrów sześciennych. Jest bardzo wygodna przy odmierzaniu płynów i niewielkich ilości materiałów. Dlatego też większość pojemników i zbiorników do użytku domowego ma podaną pojemność właśnie w litrach.

Centymetr sześcienny

Centymetr sześcienny (cm³) jest niezwykle małą jednostką objętości i stosuje się go tam, gdzie potrzebna jest wysoka precyzja. Spotkasz go w medycynie, farmacji, laboratoriach oraz motoryzacji (np. pojemność silnika). Każdy cm³ to objętość niewielkiego sześcianu o boku 1 cm, co pozwala na dokładne określanie nawet mikroskopijnych ilości substancji.

Decymetr sześcienny

Decymetr sześcienny (dm³) jest bezpośrednio powiązany z litrem – 1 dm³ to dokładnie 1 litr. Ta jednostka świetnie sprawdza się w pomiarach naukowych, technicznych i domowych, ponieważ jest wystarczająco duża, by być praktyczna, i wystarczająco precyzyjna, by unikać dużych zaokrągleń.

Metr sześcienny jako jednostka metryczna

Metr sześcienny (m³) to podstawowa jednostka objętości w układzie SI. Używa się go przy pomiarach dużych przestrzeni, jak pomieszczenia, kontenery, magazyny czy ilości materiałów sypkich. To również najważniejsza jednostka w budownictwie i transporcie, bo umożliwia ocenę faktycznej pojemności w praktycznych zastosowaniach.

Przeliczenia między jednostkami

Przeliczanie między jednostkami pozwala sprawnie zmienić litry czy centymetry sześcienne na m³ i odwrotnie. Dzięki temu możesz dopasować wyniki do wymaganej skali.

L → m³

Aby zamienić litry na metry sześcienne, podziel ich liczbę przez 1000. Wynika to z zależności 1 m³ = 1000 l. Jeśli więc masz pojemnik 250 l, jego objętość w m³ wynosi 0,25. Takie przeliczenie przydaje się szczególnie wtedy, gdy producenci podają pojemność w litrach, a Ty potrzebujesz jej w m³, np. do transportu lub obliczeń budowlanych.

cm³ → m³

Centymetry sześcienne przeliczasz na metry sześcienne, dzieląc je przez 1 000 000. To efekt różnicy skali – metr to aż sto centymetrów, a więc m³ składa się z miliona malutkich cm³. Dzięki temu możesz dokładnie przeliczyć nawet bardzo małe ilości substancji, jeśli musisz podać wynik w m³.

dm³ → m³

Aby zamienić decymetry sześcienne na metry sześcienne, podziel ich liczbę przez 1000. Ponieważ 1 dm³ = 1 l, przeliczanie jest wyjątkowo intuicyjne i bardzo przydatne w praktyce. Jeśli masz np. akwarium o pojemności 80 dm³, wystarczy podzielić tę wartość przez 1000, aby otrzymać 0,08 m³.

m³ → litry i inne jednostki

Gdy chcesz zamienić metry sześcienne na litry, pomnóż ich liczbę przez 1000. Ten krok pozwala szybko ustalić, ile płynu lub materiału zmieści się w danym zbiorniku. Jeśli potrzebujesz wartości w dm³ lub cm³, stosujesz te same zasady przeliczeń – mnożysz odpowiednio przez 1000 lub przez 1 000 000. Dzięki temu możesz dopasować jednostki do konkretnego zastosowania i uniknąć pomyłek.

Jednostka	Symbol	Relacja do 1 m³	Przeliczenie na m³	Przeliczenie z m³
Metr sześcienny	m³	—	1 m³	—
Litr	l	1000 l = 1 m³	1 l = 0,001 m³	1 m³ = 1000 l
Decymetr sześcienny	dm³	1000 dm³ = 1 m³	1 dm³ = 0,001 m³	1 m³ = 1000 dm³
Centymetr sześcienny	cm³	1 000 000 cm³ = 1 m³	1 cm³ = 0,000001 m³	1 m³ = 1 000 000 cm³
Mililitr	ml	1000 ml = 1 l = 0,001 m³	1 ml = 0,000001 m³	1 m³ = 1 000 000 ml

Objętość pomieszczenia – jak obliczyć m³ w praktyce?

Jeśli chcesz wiedzieć, jak obliczyć metry sześcienne pomieszczenia, wystarczy kilka prostych pomiarów i właściwy wzór. Dzięki temu szybko ustalisz kubaturę pokoju i dopasujesz do niej ogrzewanie, klimatyzację czy ilość potrzebnych materiałów wykończeniowych.

Pomiar długości, szerokości i wysokości

Aby obliczyć objętość pomieszczenia, zacznij od dokładnego zmierzenia trzech podstawowych wymiarów: długości, szerokości i wysokości. Najlepiej używać miarki laserowej, bo daje precyzyjniejsze wyniki, zwłaszcza w większych pokojach. Jeśli mierzysz wysokość, sprawdź ją w dwóch lub trzech punktach, bo stropy nie zawsze są idealnie równe.

Wpływ nieregularnego kształtu

Jeżeli pomieszczenie nie jest idealnym prostopadłościanem, możesz podzielić je na mniejsze, regularne części i policzyć objętość każdej z nich osobno. Skosy, wnęki czy podwyższenia łatwo uwzględnić, jeśli traktujesz je jako oddzielne bryły, np. małe prostopadłościany lub trójkątne graniastosłupy. Dzięki temu wynik będzie dokładny i użyteczny przy planowaniu wyposażenia lub obliczeń technicznych.

Przykład: obliczenie kubatury pokoju

Wyobraź sobie pokój o długości 5 m, szerokości 3,8 m i wysokości 2,6 m. Aby obliczyć jego objętość, mnożysz te trzy wartości: 5 × 3,8 × 2,6 = 49,4 m³. Taki wynik pokazuje realną przestrzeń powietrza w pomieszczeniu, co jest kluczowe np. przy wyborze odpowiedniej mocy klimatyzatora, określaniu wydajności wentylacji czy planowaniu ogrzewania. Dzięki dokładnym pomiarom masz pewność, że wszystko będzie działać optymalnie.

Praktyczne zastosowania obliczania metrów sześciennych

Wiedza o tym, jak obliczyć metry sześcienne, przydaje się w wielu codziennych i zawodowych sytuacjach. Pozwala lepiej planować przestrzeń, optymalizować koszty i podejmować decyzje oparte na realnych danych, a nie na zgadywaniu.

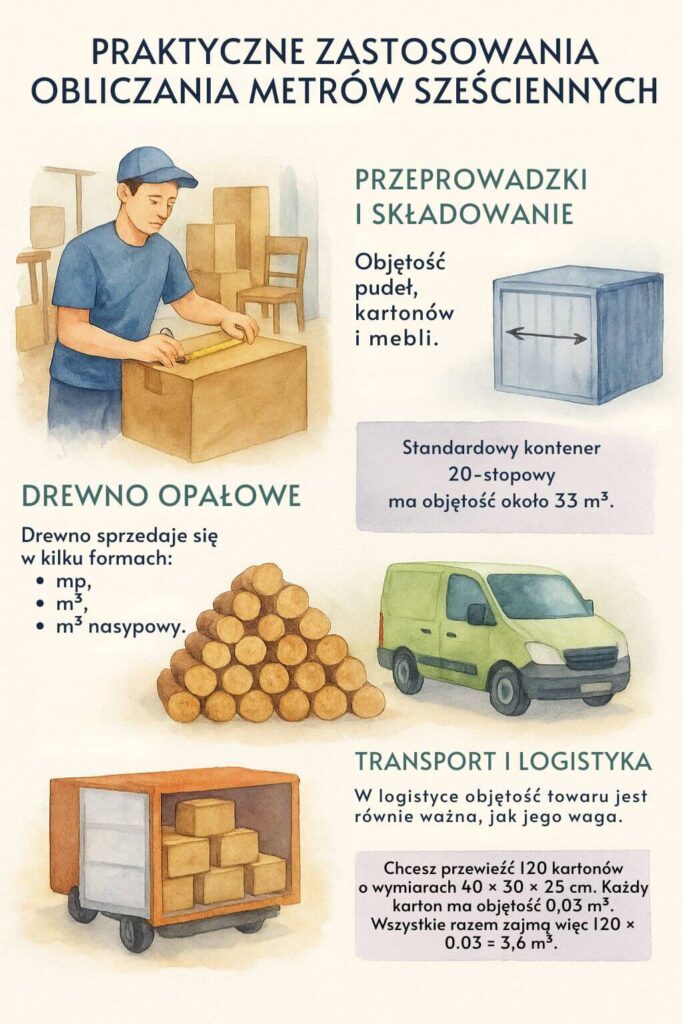
Przeprowadzki i składowanie

Podczas przeprowadzki albo organizacji magazynu umiejętność obliczenia objętości ładunku pozwala ocenić, jakiego pojazdu potrzebujesz i ile rzeczy zmieści się w danej przestrzeni.

Jak obliczać objętość ładunku?

Najpierw zmierz wymiary każdego elementu lub grup rzeczy – długość, szerokość i wysokość – a następnie przelicz je na m³. Dzięki temu możesz precyzyjnie zaplanować rozmieszczenie przedmiotów i uniknąć niepotrzebnych kursów lub wynajmu zbyt dużego pojazdu.

Objętość pudeł, kartonów i mebli

Każdy karton czy mebel można potraktować jako prostopadłościan. Jeśli któryś element ma wystające części lub nietypowy kształt, warto liczyć jego maksymalną objętość, aby mieć pewność, że zmieści się w samochodzie lub magazynie.

Przykład: kontener transportowy

Standardowy kontener 20-stopowy ma objętość około 33 m³. Jeśli Twoje rzeczy zajmują łącznie 28 m³, masz pewność, że bez problemu się zmieszczą – a jeśli wynik wynosi 34–35 m³, potrzebujesz kontenera 40-stopowego lub dwóch mniejszych.

Drewno opałowe

Przy zakupie drewna objętość jest kluczowa, bo różne jednostki mogą wprowadzać w błąd, jeśli nie wiesz, jak je przeliczać.

Różne jednostki: mp, m³, m³ nasypowe

Drewno sprzedaje się w kilku formach:

• mp (metr przestrzenny),
• m³ (metr sześcienny litego drewna),
• m³ nasypowy. 

Każda z nich oznacza inną rzeczywistą ilość materiału – szczególnie gdy drewno jest cięte lub układane luzem.

Przeliczenia drewna (np. 1 mp = 0,7–0,8 m³)

Jeśli kupujesz 1 mp drewna ułożonego w stosie, realnie otrzymujesz około 0,7–0,8 m³ litego drewna. Ta różnica wynika z pustych przestrzeni między polanami. Znajomość przeliczeń pozwala Ci ocenić, czy oferta jest uczciwa i ile drewna faktycznie dostajesz.

Jak mierzyć objętość drewna luzem i ułożonego?

Drewno luzem najlepiej mierzyć, sypiąc je do pojemnika o znanej objętości – wtedy wynik jest najdokładniejszy. Drewno ułożone w stosie warto mierzyć według wysokości, szerokości i długości stosu, a następnie pomnożyć te wartości, pamiętając o współczynniku pustych przestrzeni.

Transport i logistyka

W logistyce objętość towaru jest równie ważna, jak jego waga – decyduje o tym, czy coś zmieści się w pojeździe i jaka będzie wydajność transportu.

Objętość w m³ a ładowność pojazdu

Samochody dostawcze, naczepy i kontenery mają określone limity objętości. Często to właśnie m³, a nie kilogramy, są głównym ograniczeniem. Jeśli ładunek jest lekki, ale zajmuje dużo miejsca, możesz przekroczyć limit przestrzeni mimo niewielkiej masy.

Przykład obliczenia objętości towaru

Załóżmy, że chcesz przewieźć 120 kartonów o wymiarach 40 × 30 × 25 cm. Każdy karton ma objętość 0,03 m³. Wszystkie razem zajmą więc 120 × 0.03 = 3,6 m³. Dzięki temu możesz od razu ocenić, czy ładunek zmieści się do busa o przestrzeni 4–5 m³, bez ryzyka, że zabraknie miejsca.

Wskazówki, błędy i narzędzia pomocnicze

Warto poznać też najczęstsze pułapki oraz proste triki, które sprawiają, że obliczenia są dokładniejsze i szybsze. Dzięki temu unikniesz kosztownych pomyłek i będziesz mieć pewność, że wynik jest wiarygodny.

Najczęstsze błędy

Podczas obliczania objętości drobne niedokładności mogą prowadzić do znaczących różnic w wyniku, dlatego warto wiedzieć, na co zwracać uwagę.

Nieprawidłowe jednostki

Jednym z najczęstszych błędów jest mieszanie jednostek, np. mierzenie długości w centymetrach, szerokości w metrach, a wysokości w milimetrach. Przed obliczeniami zawsze zamień wszystkie wartości na metry, aby uniknąć zafałszowanych rezultatów.

Zaokrąglenia

Zbyt wczesne zaokrąglanie wartości potrafi zmienić wynik nawet o kilka procent. Najlepiej zaokrąglać dopiero finalny rezultat, zwłaszcza jeśli obliczasz objętość dla transportu, budowy czy zakupu materiałów.

Zły pomiar wysokości lub promienia

Wysokość pomieszczeń czy promień podstawy ma ogromne znaczenie, bo występuje w każdym wzorze. Błąd kilku centymetrów przy promieniu może zwiększyć pomyłkę nawet kilkukrotnie, ponieważ r² lub r³ mocno wzmacnia różnice.

Błędy przy konwersjach jednostek

Mylenie przeliczeń, np. traktowanie 1 l jako 0,01 m³ zamiast 0,001, to jedna z najczęstszych przyczyn błędnych obliczeń. Warto mieć pod ręką prostą tabelę konwersji lub kalkulator jednostek.

Wskazówki pomiarowe

Dokładne pomiary to podstawa prawidłowych obliczeń, szczególnie gdy zależy Ci na wysokiej precyzji.

Jak prawidłowo mierzyć?

Mierz elementy zawsze od maksymalnie wysuniętej krawędzi do krawędzi. Jeśli masz do czynienia z nieregularnym kształtem, mierz w kilku miejscach i uśredniaj wynik – to znacząco zmniejszy ryzyko błędu.

Kontrola wyniku krok po kroku

Po wykonaniu pomiarów podstaw wartości do wzoru i sprawdź, czy jednostki są jednolite. Jeśli wynik wydaje Ci się podejrzanie duży lub mały, jeszcze raz przelicz liczby. Warto też zweryfikować pomiary, zwłaszcza gdy pracujesz z dużymi przestrzeniami lub pojemnikami.

Zastosowanie taśm, przymiarów, poziomic

Tradycyjna taśma miernicza sprawdzi się przy małych i średnich elementach, ale do większych pomieszczeń warto użyć dalmierza laserowego. Poziomica pomoże upewnić się, że pomiar wysokości lub długości jest wykonany prosto i bez odchylenia.

Narzędzia do obliczania objętości

Dziś nie musisz liczyć wszystkiego ręcznie – wiele narzędzi może przyspieszyć cały proces i zminimalizować ryzyko pomyłki.

Kalkulatory online

Proste kalkulatory dostępne w sieci pozwalają szybko obliczyć objętość prostopadłościanu, walca czy kuli na podstawie wprowadzonych wymiarów. To najszybsza metoda, gdy chcesz dostać wynik bez ręcznego liczenia.

Aplikacje mobilne

Wiele aplikacji mierzy odległości przy pomocy AR lub aparatu, co pozwala w kilka chwil ustalić wymiary nawet dużych przestrzeni. Idealne podczas przeprowadzek, remontów czy zakupów materiałów.

Arkusze kalkulacyjne

Excel, Google Sheets czy LibreOffice Calc pozwalają tworzyć własne kalkulatory objętości. Wprowadzasz wzory raz i możesz korzystać z nich wielokrotnie, zapisując wyniki lub porównując różne warianty.

Wyszukiwarki internetowe

Wystarczy wpisać w wyszukiwarkę „kalkulator objętości” albo nawet sam wzór, aby natychmiast otrzymać wynik. To wygodne rozwiązanie, gdy potrzebujesz szybkiego przeliczenia na telefonie lub komputerze.

Podsumowanie

Teraz wiesz już, jak obliczyć metry sześcienne w każdej praktycznej sytuacji – od pomiaru pokoju, przez obliczanie objętości ładunku, aż po przeliczanie jednostek czy zakup drewna opałowego. Kluczem jest dokładny pomiar, właściwy wzór i jednolite jednostki. Dzięki temu Twoje obliczenia będą pewne, a decyzje bardziej świadome i opłacalne.

FAQ – najczęściej zadawane pytania

Jak obliczyć metry sześcienne pomieszczenia?

Wystarczy pomnożyć długość, szerokość i wysokość wyrażone w metrach. Jeśli pokój ma nieregularny kształt, podziel go na mniejsze bryły i policz każdą osobno.

Ile to jest 1 m³ w litrach?

1 m³ to dokładnie 1000 litrów.

Jak obliczyć objętość walca lub rury?

Użyj wzoru V = πr²h, gdzie r to promień podstawy (połowa średnicy), a h to wysokość lub długość rury.

Jak przeliczyć litry na metry sześcienne?

Podziel liczbę litrów przez 1000. Np. 250 l to 0,25 m³.

Co zrobić, jeśli obiekt ma nieregularny kształt?

Najlepiej podzielić go na możliwie najprostsze bryły geometryczne (np. prostopadłościany, walce) i policzyć objętość każdej z nich.

Jak uniknąć błędów przy obliczeniach?

Używaj jednolitych jednostek (najlepiej metrów), nie zaokrąglaj zbyt wcześnie i pamiętaj o dokładnych pomiarach – szczególnie wysokości i promienia.

Czy istnieją narzędzia, które zrobią to za mnie?

Tak, kalkulatory online, aplikacje mobilne i arkusze kalkulacyjne pozwalają błyskawicznie obliczyć objętość dowolnego obiektu.

Bibliografia

1. https://www.omnicalculator.com/pl/przeliczniki/kalkulator-metrow-szesciennych
2. https://zpe.gov.pl/a/objetosc-prostopadloscianu/D69vUcRhw
3. https://www.matemaks.pl/walec.html
4. https://www.matemaks.pl/stozek.html
5. https://www.matemaks.pl/kula.html
6. https://www.metric-conversions.org/pl/objetosc/metry-szescienne-do-litry.htm
7. https://wodnykalkulator.pl/m3-ile-to-litrow-poznaj-tabele-przelicznikow/
8. https://www.metric-conversions.org/pl/objetosc/cale-szescienne-do-centymetry-szescienne.htm
9. https://form.pl/artykuly/jak-obliczyc-objetosc-v/
10. https://www.ogrzewnictwo.pl/artykuly/paliwa/drewno/pomiar-objetosci-drewna-opalowego
11. https://ladnydom.pl/1-metr-przestrzenny-ile-to-m3-metr-przestrzenny-a-metr-szescienny-kubik